A floating object is displacing fluids that would otherwise fill the space it occupies. For example, a ball floating motionless on water is displacing the water and air that would normally be where the ball is. If we remove the ball, water and air will fill its space and soon everything will be motionless again.
Just because that ball-shaped portion of water and air is motionless doesn’t mean that it’s weightless. It does have a weight! But its weight is supported by the water and air that surround it. Because of the earth’s gravity, the pressure of stationary water or air decreases steadily with altitude, so pressure exerted on the bottom of this ball-shaped portion is greater than the pressure exerted on its top. This unbalanced pressure produce a net upward force on the ball-shaped portion of water and air.
That upward force is known as the buoyant force and it’s evidently just strong enough to support the weight of the ball-shaped portion of water and air. If it weren’t the ball-shaped portion would accelerate up or down.
When we put the real ball back where it was and let it again float motionless on the water, the surrounding water and air continue to exert the same buoyant force on the real ball that they exerted on the ball-shaped portion of water and air. So the ball experiences an upward buoyant force that’s equal in amount to the weight of the water and air it displaces. That observation is known as Archimedes’ principle.
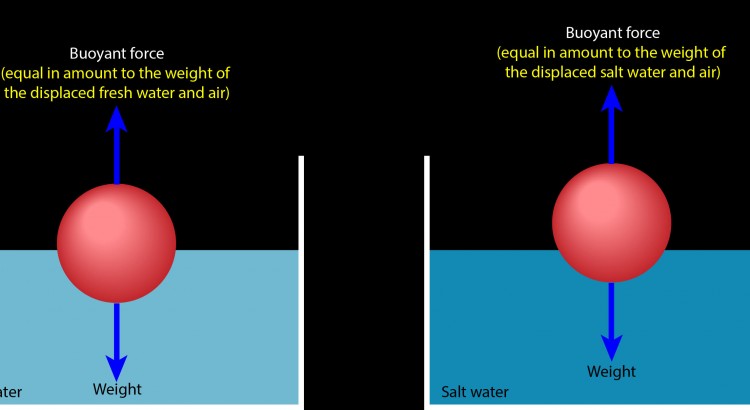
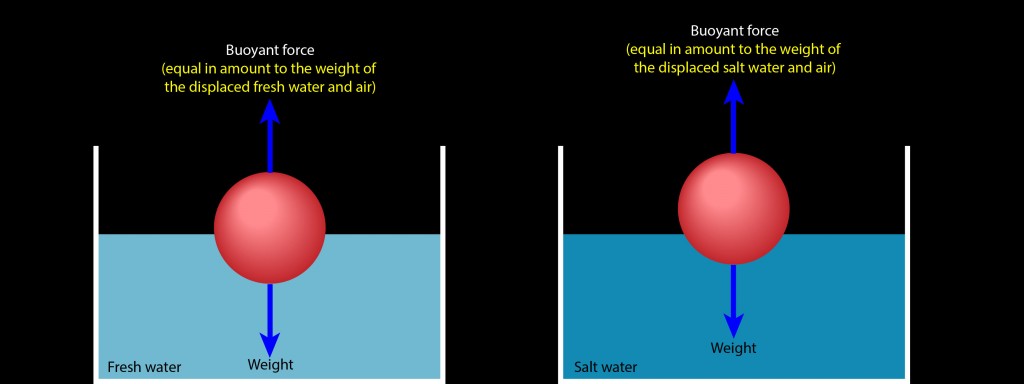
Which brings me to your question. Here are two identical balls floating motionless on fresh water (left) and on salt water (right). In each case, the ball is experiencing a buoyant force that exactly cancels its weight. To obtain that exact buoyant force, the ball must displace a portion of water and air that weighs exactly as much as the ball weighs.
Salt water is denser than fresh water, meaning that salt water has more mass per volume (more kilograms per liter) than fresh water. A liter of salt water consequently weighs more than a liter of fresh water. Displacing a liter of salt water therefore produces a stronger upward buoyant force than displacing a liter of fresh water. That’s why the ball is floating higher on the container of salt water than it does on the container of fresh water.
The ball doesn’t need to displace as much salt water to obtain a buoyant force that supports its weight, so it rises higher on the salt water than it does on the fresh water. In each case, the ball finds just the right mix of water and air so that it displaces exactly its own weight in those two fluids.